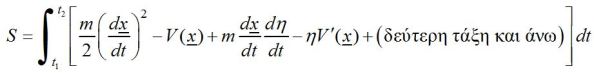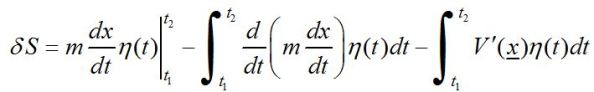Μια μέρα όταν ήμουν ακόμα μαθητής στο Λύκειο ο καθηγητής μου της Φυσικής – ο κ. Bader – με φώναξε μετά το μάθημα και μου είπε:
«Φαίνεται ότι βαριέσαι κατά τη διάρκεια του μαθήματος, γι αυτό θα θελα να σου πω κάτι που το θεωρώ ενδιαφέρον». Αυτό που μου είπε αμέσως μετά το βρήκα απόλυτα συναρπαστικό, τόσο που εξακολουθεί να με συναρπάζει μέχρι και σήμερα. Το θέμα αυτό εμφανίζεται συνέχεια μπροστά μου και δουλεύω πάνω σ’ αυτό διαρκώς. Για να είμαι ειλικρινής, στην πραγματικότητα, όσο προετοίμαζα την συγκεκριμένη διάλεξη συνέλαβα τον εαυτό μου να κάνει επιπλέον αναλύσεις στο συγκεκριμένο ζήτημα. Αντί να ανησυχώ για τη διάλεξη προτίμησα να μπλεχτώ μ’ ένα καινούργιο πρόβλημα. Και το θέμα που με απορροφά δεν είναι άλλο από την αρχή της ελάχιστης δράσης.
Ο κ. Bader μου είπε τα ακόλουθα:
«Έστω σωματίδιο που βρίσκεται π.χ. σε βαρυτικό πεδίο, το οποίο ξεκινάει από κάποιο σημείο για να καταλήξει σε κάποιο άλλο, κινούμενο ελεύθερα – π.χ. το πετάμε προς τα πάνω και μετά από κάποια χρονική στιγμή αρχίζει να πέφτει προς τα κάτω. Η μετακίνηση από την αρχική έως την τελική θέση πραγματοποιείται σε συγκεκριμένο χρονικό διάστημα (t2 – t1).
Τώρα, δοκιμάζουμε ένα διαφορετικό – υποθετικό – είδος κίνησης: «Έστω ότι η μετάβαση από το σημείο (Α) στο σημείο (Β) έγινε μεν στο ίδιο χρονικό διάστημα (t2 – t1) αλλά η τροχιά του σωματιδίου είναι αυτή που σχεδιάσαμε στο δεύτερο σχήμα» και συνέχισε: «Αν υπολογίσεις την κινητική ενέργεια για κάθε χρονική στιγμή της διαδρομής, αφαιρέσεις την δυναμική ενέργεια και ολοκληρώσεις για το χρονικό διάστημα της διαδρομής, το αποτέλεσμα που θα βρεις θα είναι μεγαλύτερο από αυτό της πραγματικής κίνησης του σωματιδίου που περιγράφεται στο πρώτο σχήμα».
Μ’ άλλα λόγια…..οι νόμοι του Νεύτωνα, αντί να βασιστούν στον τύπο:
F = m · α
θα μπορούσαν ισοδύναμα να βασιστούν στην πρόταση:
«Κατά τη διαδρομή ενός σώματος που μετακινείται από ένα σημείο σε ένα άλλο, διαφορά της μέσης κινητικής ενέργειας από την μέση δυναμική ενέργεια έχει την ελάχιστη δυνατή τιμή».
Επιτρέψτε μου να ερμηνεύσω κάπως καλύτερα το νόημά της:
Στο παράδειγμα του βαρυτικού πεδίου αν το σωματίδιο ακολουθεί τη διαδρομή x(t), (ας αρκεστούμε σε μονοδιάστατη κίνηση θεωρούμε την τροχιά προς τα πάνω και της κίνησης προς τα κάτω που ακολουθεί (χωρίς να μετακινείται πλευρικά, είτε δεξιά είτε αριστερά) όπου x είναι το ύψος, η απόσταση από το έδαφος, τότε η κινητική ενέργεια είναι
και η δυναμική ενέργεια είναι: m g x.
Στη συνέχεια θεωρώ την διαφορά κινητικής – δυναμικής ενέργειας για κάθε χρονική στιγμή της διαδρομής και ολοκληρώνω ως προς τον χρόνο, από την αρχική χρονική στιγμή έως την τελική χρονική στιγμή. Υποθέτουμε ότι την χρονική στιγμή t1 αρχίζει η κίνηση σε κάποιο ύψος από το έδαφος και τη χρονική στιγμή t2 φθάνει σε κάποιο άλλο σημείο.
Τότε το ολοκλήρωμα έχει τη μορφή
Η πραγματική κίνηση είναι κάποια καμπύλη τροχιά – είναι παραβολή αν κάνουμε την γραφική παράσταση συναρτήσει του χρόνου – και φυσικά δίνει συγκεκριμένη τιμή για το ολοκλήρωμά μας.
Αλλά θα μπορούσαμε να «φανταστούμε» μια διαφορετική κίνηση: το σωματίδιο πήγε πολύ ψηλά και μετά ανεβοκατέβηκε κατά ένα παράδοξο τρόπο.
Μπορούμε φυσικά να υπολογίσουμε το αντίστοιχο ολοκλήρωμα για μια τέτοια διαδρομή ή για οποιαδήποτε άλλη διαδρομή επιθυμούμε. Το θαύμα έγκειται στο ότι η ελάχιστη τιμή του συγκεκριμένου ολοκληρώματος αντιστοιχεί στην πραγματική διαδρομή και μόνο σ’ αυτή.
Ας το δοκιμάσουμε: Αρχικά θεωρούμε ελεύθερο σώμα με μηδενική δυναμική ενέργεια. Τότε ισχύει ότι κατά τη διαδρομή του από ένα σημείο σε κάποιο άλλο, η τιμή του ολοκληρώματος της κινητικής ενέργειας (για συγκεκριμένο χρονικό διάστημα) είναι η ελάχιστη έτσι ώστε να κινείται με σταθερή ταχύτητα. (Είναι γνωστό ότι αυτή είναι η σωστή απάντηση – κίνηση με σταθερή ταχύτητα). Και γιατί με σταθερή ταχύτητα; Γιατί αν το σώμα εκτελούσε οποιαδήποτε άλλη κίνηση, οι ταχύτητες θα είχαν τιμές πότε υψηλότερες και πότε χαμηλότερες από τη μέση τιμή. Η μέση ταχύτητα έχει την ίδια τιμή σε κάθε περίπτωση γιατί το σώμα πρέπει να εκτελέσει μια συγκεκριμένη διαδρομή σε συγκεκριμένο χρόνο.
Για παράδειγμα, υποθέστε ότι η δουλειά σας είναι να ξεκινάτε με αυτοκίνητο από το σπίτι και να φτάσετε στο σχολείο σε συγκεκριμένο χρονικό διάστημα. Μπορείτε να το κάνετε με διάφορους τρόπους: Για παράδειγμα, μπορείτε να επιταχύνετε σαν τρελοί και μετά να πατάτε απότομα το φρένο σχεδόν τέρμα ή να πηγαίνετε με σταθερή ταχύτητα ή ακόμα να βάζετε την όπισθεν για λίγο και μετά να κινείστε ξανά προς τα εμπρός κ.λ.π. Όποιο είδος κίνησης και να διαλέξετε είναι γεγονός ότι η μέση ταχύτητα θα είναι πάντα το πηλίκο της συνολικής διαδρομής προς τον αντίστοιχο χρόνο. Όμως αν επιλέξετε οτιδήποτε άλλο εκτός από την κίνηση με σταθερή ταχύτητα, τότε είναι βέβαιο ότι θα κινείστε πότε γρήγορα και πότε αργά. Ξέρετε όμως ότι η μέση τιμή του τετραγώνου κάποιου μεγέθους που αποκλίνει του μέσου όρου είναι πάντα μεγαλύτερη του τετραγώνου της μέσης τιμής του. Έτσι το ολοκλήρωμα της κινητικής ενέργειας θα πρέπει να είναι πάντα μεγαλύτερο αν η τιμή της ταχύτητάς μας αυξομειώνεται σε σχέση με το ολοκλήρωμα όπου η ταχύτητα είναι σταθερή. Επομένως το ολοκλήρωμα είναι ελάχιστο αν η ταχύτητα είναι σταθερή (και η συνισταμένη δύναμη ίση με μηδέν). Η σωστή διαδρομή δίνεται στο σχήμα.
Τώρα, όταν πετάμε ένα αντικείμενο προς τα πάνω (σε βαρυτικό πεδίο) κινείται στην αρχή γρήγορα και μετά επιβραδύνεται. Αυτό οφείλεται στην ύπαρξη της δυναμικής ενέργειας και στο ότι πρέπει να έχουμε ελάχιστη διαφορά δυναμικής και κινητικής ενέργειας. Εφόσον η τιμή της δυναμικής ενέργειας αυξάνεται όσο ανεβαίνουμε προς τα πάνω, θα επιτύχουμε την ελάχιστη τιμή της διαφοράς εάν φτάσουμε στο σημείο της μέγιστης δυναμικής ενέργειας το συντομότερο δυνατόν. Μετά μπορούμε να αφαιρέσουμε την δυναμική από την κινητική ενέργεια και να έχουμε ένα χαμηλότερο μέσο όρο. Άρα είναι προτιμότερη μια διαδρομή ανόδου που παίρνει αρκετή αρνητική ποσότητα από τη δυναμική ενέργεια.
Από την άλλη πλευρά, δεν μπορούμε να ανεβούμε πολύ γρήγορα γιατί θα απαιτηθεί μεγάλο ποσό κινητικής ενέργειας – θα πρέπει να κινούμαστε πολύ γρήγορα κατά την άνοδο και να προλάβουμε να κατεβούμε κατά την διάρκεια του διαθέσιμου χρόνου. Δεν θέλουμε επομένως να ανεβούμε σε πολύ μεγάλο ύψος. Συμπεραίνουμε λοιπόν ότι η λύση είναι ένα είδος ισορροπίας μεταξύ της προσπάθειας να κερδίσουμε όση περισσότερη δυναμική ενέργεια μπορούμε χρησιμοποιώντας την ελάχιστη δυνατή επιπλέον κινητική ενέργεια – προσπαθώντας πάντα να διατηρούμε την διαφορά της κινητικής μείον την δυναμική ενέργεια όσο μικρότερη γίνεται.
Αυτά ήταν όλα όσα μου είπε ο δάσκαλός μου. Ήταν ένας πολύ καλός δάσκαλος που ήξερε πότε έπρεπε να σταματήσει να μιλάει. Όμως εγώ δεν ξέρω πότε πρέπει να σταματήσω να μιλάω. Γι’ αυτό αντί να σταματήσω σ’ αυτή την ενδιαφέρουσα παρατήρηση σκοπεύω να σας τρομοκρατήσω μέχρι αηδίας με την πολυπλοκότητα της ζωής αποδεικνύοντας την ορθότητά της. Το μαθηματικό πρόβλημα που αντιμετωπίζουμε είναι πολύ δύσκολο και είναι ένα νέο είδος. Έχουμε μια συγκεκριμένη ποσότητα που την ονομάζουμε δράση (S). Είναι το ολοκλήρωμα ως προς τον χρόνο της διαφοράς της κινητικής μείον την δυναμική ενέργεια:
Θυμηθείτε ότι τόσο η κινητική όσο και η δυναμική ενέργεια είναι συναρτήσεις του χρόνου. Για κάθε διαφορετική πιθανή διαδρομή έχουμε και διαφορετική τιμή για την δράση (S). Το μαθηματικό πρόβλημα είναι να ανακαλύψουμε για ποια καμπύλη η τιμή αυτή είναι ελάχιστη. Θα μου πείτε – Μα δεν είναι παρά η συνηθισμένη διαδικασία για τα μέγιστα και τα ελάχιστα. Υπολογίζουμε την δράση (S) και απλώς διαφορίζουμε για να βρούμε το ελάχιστο.
Προσέξτε όμως: κανονικά έχουμε την συνάρτηση κάποιας μεταβλητής και απλώς θέλουμε να βρούμε την τιμή της μεταβλητής αυτής όταν η συνάρτηση γίνεται ελάχιστη ή μέγιστη. Για παράδειγμα, έχουμε μια ράβδο που την θερμαίνουμε στο μέσον της και βέβαια η θερμότητα διαχέεται τριγύρω. Για κάθε σημείο της ράβδου έχουμε μια θερμοκρασία και πρέπει να βρούμε το σημείο της ράβδου στο οποίο η θερμοκρασία είναι μέγιστη.
Στην περίπτωσή μας όμως, για κάθε διαδρομή στο χώρο έχουμε μια τιμή – εντελώς διαφορετική περίπτωση – και πρέπει να βρούμε την διαδρομή στο χώρο για την οποία η τιμή αυτή είναι ελάχιστη. Στην πραγματικότητα η διαδικασία αυτή λέγεται «Λογισμός των μεταβολών».
Υπάρχουν πολλά προβλήματα σ’ αυτό το είδος των μαθηματικών. Για παράδειγμα, ο κύκλος ορίζεται ως τόπος όλων των σημείων που απέχουν σταθερή απόσταση από δεδομένο σημείο. Όμως υπάρχει και διαφορετικός ορισμός του κύκλου: κύκλος είναι η καμπύλη δεδομένου μήκους η οποία περικλείει το μέγιστο εμβαδόν. Οποιαδήποτε άλλη καμπύλη περικλείει μικρότερο εμβαδόν για δεδομένη περίμετρο απ’ ότι ο κύκλος. Έτσι, αν δώσουμε το πρόβλημα: Βρείτε την καμπύλη η οποία περικλείει το μέγιστο εμβαδόν για δεδομένη περίμετρο, θα είχαμε ένα πρόβλημα λογισμού των μεταβολών, ένα πρόβλημα διαφορετικό από αυτά που έχουμε συνηθίσει.
Επομένως προχωρούμε σε υπολογισμούς που αφορούν την διαδρομή ενός αντικειμένου, με τον ακόλουθο τρόπο: Η κεντρική ιδέα είναι ότι θεωρούμε πως υπάρχει μια και μόνο μια πραγματική διαδρομή και ότι οποιαδήποτε άλλη καμπύλη και να σχεδιάσουμε είναι λανθασμένη. Έτσι, αν υπολογίσουμε την δράση για την λανθασμένη διαδρομή θα πάρουμε μια τιμή που θα είναι μεγαλύτερη από αυτή της σωστής διαδρομής.
«Άσκηση: Βρείτε την πραγματική διαδρομή». Που βρίσκεται; Φυσικά ένας τρόπος είναι να υπολογίσουμε την δράση για εκατομμύρια διαδρομών και να εντοπίσουμε την ελάχιστη τιμή. Όταν την βρούμε έχουμε και την αντίστοιχη πραγματική διαδρομή.
Αυτός είναι ένας τρόπος επίλυσης του προβλήματος. Όμως μπορούμε να τα καταφέρουμε και καλύτερα.
Όταν έχουμε μια ποσότητα που έχει ελάχιστο – για παράδειγμα μια συνηθισμένη συνάρτηση όπως η θερμοκρασία – μια από τις ιδιότητες της ελάχιστης τιμής είναι ότι αν απομακρυνθούμε από αυτήν με προσέγγιση 1ης τάξης τότε η απόκλιση είναι μόνο δεύτερης τάξης. Σε οποιοδήποτε άλλο σημείο της καμπύλης, αν μετακινηθούμε για πολύ μικρή απόσταση η μεταβολή της τιμής της συνάρτησης είναι 1ης τάξης. Αλλά στο ελάχιστο, μια μικρή μετακίνηση δεν φέρνει, σε πρώτη προσέγγιση, καμιά διαφορά.

Αυτό ακριβώς θα χρησιμοποιήσουμε για να βρούμε την πραγματική διαδρομή. Αν έχουμε την πραγματική διαδρομή, τότε μια καμπύλη που θα αποκλίνει ελάχιστα από αυτήν δεν θα αντιστοιχεί, σε πρώτη προσέγγιση σε διαφορετική τιμή δράσης. Οποιαδήποτε διαφορά θα μπορεί να εντοπιστεί στην δεύτερη προσέγγιση αν έχουμε βρει πραγματικά την ελάχιστη τιμή.
Αυτό αποδεικνύεται εύκολα: Αν υπάρχει μεταβολή στην προσέγγιση πρώτης τάξης όταν αποκλίνει η καμπύλη, τότε υπάρχει μεταβολή και στην δράση, η οποία είναι ανάλογη της απόκλισης. Η μεταβολή προφανώς αυξάνει την δράση, αλλιώς δεν είμαστε στην ελάχιστη τιμή της συνάρτησης. Αν όμως η μεταβολή είναι ανάλογη της απόκλισης, τότε αν αντιστρέψω την φορά της απόκλισης η δράση μειώνεται. θα έπρεπε λοιπόν η τιμή της δράσης να αυξάνεται κατά την μια κατεύθυνση και να μειώνεται από την άλλη. Η μόνη περίπτωση να έχουμε πράγματι την ελάχιστη τιμή είναι να μην παρατηρείται μεταβολή στην πρώτη προσέγγιση και οι μεταβολές να είναι ανάλογες του τετραγώνου της απόκλισης από την πραγματική διαδρομή.
Προχωρούμε λοιπόν ως εξής: Ονομάζουμε x(t) την πραγματική διαδρομή – αυτή που προσπαθούμε να βρούμε. Μετά θεωρούμε μια δοκιμαστική διαδρομή x(t) η οποία διαφέρει ελάχιστα από την πραγματική κατά μια ποσότητα που ονομάζουμε η(t). Το σκεπτικό μας είναι ότι αν υπολογίσουμε την δράση S για την διαδρομή x(t) τότε η διαφορά της από την δράση που αντιστοιχεί στην πραγματική διαδρομή x(t) – για λόγους απλούστευσης την συμβολίζουμε με S – η διαφορά λοιπόν μεταξύ S και S πρέπει να είναι μηδέν για μια προσέγγιση 1ης τάξης όταν το η(t) είναι μικρό. Θα υπάρχει διαφορά σε μια προσέγγιση δεύτερης τάξης, αλλά στην προσέγγιση 1ης τάξης πρέπει να είναι μηδέν.
Και αυτό πρέπει να ισχύει για οποιαδήποτε τιμή του η; Όχι ακριβώς. Η μέθοδος αυτή δεν ισχύει παρά μόνο για διαδρομές οι οποίες αρχίζουν και τελειώνουν σε δυο συγκεκριμένα άκρα – κάθε διαδρομή αρχίζει από ένα συγκεκριμένο σημείο σε χρόνο t1 και τελειώνει σε χρόνο t2 και αυτά τα σημεία καθώς και οι χρονικές στιγμές t1 και t2 είναι αυστηρά καθορισμένα. Έτσι οι αποκλίσεις για τις τιμές μας του πρέπει να είναι μηδέν σε κάθε άκρο:η(t1) = 0 και η(t2) = 0. Με αυτή την συνθήκη έχουμε προσδιορίσει το μαθηματικό μας πρόβλημα.
Ακόμη και αν δεν γνωρίζατε διαφορικό λογισμό, θα μπορούσατε να ακολουθήσετε την ίδια μέθοδο για να βρείτε το ελάχιστο μιας συνηθισμένης συνάρτησης f(x). Θα μπορούσατε να προβληματιστείτε για το τι συμβαίνει αν προσθέσετε στο x μια μικρή ποσότητα η και να υποστηρίξετε ότι η διόρθωση στην f(x) σε προσέγγιση 1ης τάξης στο η πρέπει να είναι μηδέν όταν είμαστε στην ελάχιστη τιμή. Θα έπρεπε να αντικαταστήσετε το x με το (x+η) και να αναπτύξετε σε προσέγγιση 1ης τάξης ως προς η, ακριβώς όπως θα κάνουμε τώρα με την ποσότητα η.
Το σκεπτικό μας είναι να αντικαταστήσουμε το
x(t)=x(t)+η(t)
στον τύπο που μας δίνει την δράση:
όπου V(x) η δυναμική ενέργεια.
Η παράγωγος dx/dt είναι φυσικά η παράγωγος του x(t) συν την παράγωγο του η(t). Τελικά η δράση S δίνεται από την σχέση:
Γράφοντας την σχέση πιο αναλυτικά, έχω για την παράσταση που είναι υψωμένη στην δεύτερη δύναμη:
Μια στιγμή όμως: Δεν ανησυχώ για προσεγγίσεις μεγαλύτερες από αυτές της 1ης τάξης, γι αυτό και θα μαζέψω όλους τους όρους που περιέχουν το τετράγωνο του η ή και μεγαλύτερες δυνάμεις και θα τους τοποθετήσω σ’ ένα μικρό «κουτάκι» που θα το ονομάζω «δεύτερη τάξη και άνω». Για την συγκεκριμένη περίπτωση έχω μόνο δεύτερη τάξη, αλλά σ’ άλλες περιπτώσεις μπορεί , αλλά σ’ άλλες περιπτώσεις μπορεί να εμφανιστεί κάτι παραπάνω. Τελικά η έκφραση της κινητικής ενέργειας γίνεται:
Tώρα χρειαζόμαστε την δυναμική ενέργεια για την τιμή (x+η). Θεωρώ το η μικρό και έτσι μπορώ να γράψω την δυναμική ενέργεια σε σειρά Taylor. Είναι κατά προσέγγιση V(x), στην επόμενη προσέγγιση (από την συνήθη φύση των παραγώγων) η διόρθωση είναι η φορές ο ρυθμός μεταβολής του V ως προς x:
Συμβολίζω την παράγωγο του V ως προς x με V’ για οικονομία.. Οι όροι από το η στο τετράγωνο και πέρα ανήκουν στην κατηγορία «δεύτερη τάξη και άνω» και δεν χρειάζεται να ασχοληθούμε άλλο μαζί τους. Συνδυάζοντας τις παραπάνω σχέσεις έχουμε τελικά για την δράση:
Κοιτάζοντας προσεκτικά την παραπάνω σχέση βλέπουμε ότι οι δυο πρώτοι όροι εκφράζουν την δράση S που θα είχα υπολογίσει για την πραγματική διαδρομή x. Το σημείο που θέλω να τονίσω είναι η μεταβολή στο S – η διαφορά μεταξύ S και S που θα παίρναμε για την πραγματική διαδρομή. Την διαφορά αυτή την συμβολίζουμε με δS, δηλαδή η μεταβολή του S. Παραλείποντας τους όρους «δεύτερης τάξης και άνω» έχω για το δS :
Τώρα το πρόβλημα έχει ως εξής: Έχουμε ένα συγκεκριμένο ολοκλήρωμα. Δεν γνωρίζω ακόμα ποιο είναι το x, εκείνο όμως που οπωσδήποτε γνωρίζω είναι ότι ανεξάρτητα από την τιμή του η, το ολοκλήρωμα πρέπει να είναι ίσο με το μηδέν. Επομένως, θα σκεφτείτε, ο μόνος τρόπος για να αληθεύει αυτό είναι οποιοδήποτε γινόμενο του η να είναι ίσο με το μηδέν. Τι γίνεται όμως με τον πρώτο όρο που περιέχει τον όρο dη/dt; Αν όμως, επιτέλους, το η μπορεί να πάρει οποιαδήποτε τιμή, το ίδιο συμβαίνει και με την παράγωγό του. Έτσι, καταλήγετε στο συμπέρασμα ότι ο συντελεστής του dη/dt πρέπει να είναι επίσης ίσος με μηδέν. Αυτό δεν είναι εντελώς σωστό. Και δεν είναι απόλυτα σωστό γιατί υπάρχει σχέση μεταξύ του η και της παραγώγου του. Δεν είναι απολύτως ανεξάρτητα γιατί το η(t) πρέπει να είναι μηδέν τόσο την χρονική στιγμή t1 όσο και την χρονική στιγμή t2.
Η μέθοδος επίλυσης όλων των προβλημάτων στον λογισμό των μεταβολών βασίζεται πάνω στην ίδια γενική αρχή. Πραγματοποιείτε την μετάθεση στον όρο που θέλετε να μεταβάλετε (όπως κάναμε εδώ προσθέτοντας το η), ελέγχετε τους όρους πρώτης τάξης και μετά πάντοτε τακτοποιείτε την μετάθεση η, χωρίς όμως άλλες παραγώγους (χωρίς dη/dt). Πρέπει να ξαναγράψετε με τέτοιο τρόπο ώστε να είναι πάντα «κάτι» επί η. Θα αντιληφθείτε αμέσως την σημασία του. (Φυσικά υπάρχουν τύποι και μέθοδοι που σας λένε πως ακριβώς να κάνετε αυτή τη διαδικασία αλλά δεν είναι αρκετά γενικοί ώστε να αξίζει να ασχοληθούμε μαζί τους. Ο καλύτερος τρόπος είναι να διαφορίζουμε με τον παραπάνω τρόπο).
Πως μπορώ να ξαναγράψω τον όρο dη/dt έτσι ώστε να περιέχει το η; Μπορώ να το πετύχω ολοκληρώνοντας κατά ομάδες. Αν έχετε μια συνάρτηση f(t) πολλαπλασιασμένη με τον παράγοντα dη/dt , γράφετε την παράγωγο της (η · f ):
Το ολοκλήρωμα που θέλετε αφορά τον τελευταίο όρο και έτσι:
Στον δικό μας τύπο του δS, η συνάρτηση f είναι το γινόμενο (m· dx/dt )
Επομένως ο τύπος για το δS γίνεται:
Ο πρώτος όρος πρέπει να υπολογιστεί για t = t1 και t2. Μετά πρέπει να έχω το ολοκλήρωμα από το υπόλοιπο της ολοκλήρωσης κατά ομάδες. Ο τελευταίος όρος ξαναγράφετε χωρίς αλλαγές.
Και τώρα κάτι που συμβαίνει πάντα: Το κομμάτι που ολοκληρώσαμε εξαφανίζεται. (Στην πραγματικότητα δεν εξαφανίζεται, απλώς επαναδιατυπώνετε τις αρχικές σχέσεις μέχρι να σιγουρευτείτε ότι θα συμβεί!). Έχουμε ήδη πει ότι το η πρέπει να είναι μηδέν και στα δυο άκρα της διαδρομής, γιατί η αρχική παραδοχή είναι ότι η δράση είναι ελάχιστη με την προϋπόθεση ότι η μεταβληθείσα διαδρομή είναι μεταξύ δυο επιλεγμένων σημείων. Η συνθήκη επιβάλλει
η(t1) = η(t2) = 0
Επομένως ο όρος που ολοκληρώθηκε είναι μηδέν. «Μαζεύοντας» του υπόλοιπους όρους έχουμε για το την έκφραση:
Η μεταβολή στην τιμή του S πήρε επιτέλους την μορφή που επιδιώκαμε – υπάρχει η ποσότητα στην παρένθεση, έστω f, πολλαπλασιασμένη με το η(t) και όλο αυτό το γινόμενο ολοκληρώνεται από t1 έως t2.
Έστω ότι το ολοκλήρωμα μιας συνάρτησης F(t) επί η(t) είναι πάντοτε ίσο με το μηδέν:
Έχω μια συνάρτηση του t. Την πολλαπλασιάζω επί η(t) και ολοκληρώνω από το ένα άκρο στο άλλο. Και ανεξάρτητα από την μορφή του η(t) το ολοκλήρωμα είναι πάντα μηδέν. Τούτο σημαίνει ότι η συνάρτηση F(t) είναι μηδέν. Φαίνεται προφανές αλλά όπως και να έχει θα σας εκθέσω κάποιο είδος απόδειξης. Υποθέστε ότι επιλέγω ως η(t) κάποια συνάρτηση της οποίας η τιμή είναι πάντοτε μηδέν εκτός από μια συγκεκριμένη περιοχή πολύ κοντά σε μια επίσης συγκεκριμένη τιμή του t. Παραμένει μηδέν ώσπου να φτάνει στην συγκεκριμένη τιμή του t οπότε ανεβοκατεβαίνει στιγμιαία. Όταν υπολογίζουμε το ολοκλήρωμα του γινομένου η(t) επί οποιαδήποτε συνάρτηση f, το μοναδικό σημείο που μπορούμε να πάρουμε τιμή διάφορη του μηδενός, είναι το σημείο που η συνάρτηση η(t) «ανεβοκατεβαίνει» στιγμιαία. Κατόπιν έχουμε την τιμή του γινομένου της συνάρτησης f στο σημείο αυτό επί την τιμή του ολοκληρώματος στην περιοχή «αναπήδησης». Εκεί η τιμή του ολοκληρώματος δεν είναι μηδέν αλλά όταν πολλαπλασιάζεται με την συνάρτηση f πρέπει να μηδενίζεται, πράγμα που σημαίνει ότι η f(t) πρέπει να είναι μηδέν στο σημείο «αναπήδησης». Αλλά το σημείο αυτό μπορεί να είναι οπουδήποτε επιθυμούμε να είναι, επομένως η συνάρτηση f είναι πάντοτε μηδέν.
Βλέπουμε ότι αν το ολοκλήρωμα είναι μηδέν για οποιοδήποτε η, τότε ο συντελεστής του η πρέπει να είναι μηδέν. Το ολοκλήρωμα της δράσης S θα είναι ελάχιστο για την διαδρομή που ικανοποιεί την εξής πολύπλοκη διαφορική εξίσωση:
Στην πραγματικότητα δεν είναι τόσο περίπλοκη, την έχετε ξαναδεί: είναι ακριβώς η εξίσωση
Ο πρώτος όρος είναι το γινόμενο της μάζας επί την επιτάχυνση και ο δεύτερος είναι η παράγωγος της δυναμικής ενέργειας, που μας δίνει τη δύναμη F.
Έτσι, όσον αφορά τουλάχιστον τα διατηρητικά συστήματα, δείξαμε ότι η αρχή της ελάχιστης δράσης δίνει την σωστή απάντηση: Μας λέει ότι η διαδρομή ελάχιστης δράσης υπακούει στον νόμο του Νεύτωνα.
Απόσπασμα από το «The Feynman Lectures on Physics», Volume II, 1964 Αddison-Wesley Publishing Company Inc